Investigation on the non-homogeneity of residual stress field induced by lasershock peening

作者：Yongxiang Hu , Chunming Gong , Zhenqiang Yao , Jun Hu

Doi：10.1016/j.surfcoat.2009.04.029

期刊：Surface & Coatings Technology

摘要：激光冲击强化可在靶材中产生压缩残余应力，是一种类似于喷丸强化的新型表面处理技术。但当激光强度超过阈值时，激光冲击区域中心的残余应力将低于中心以外的残余应力。这一现象与目标材料在处理过程中快速而复杂的反应密切相关。作为研究冲击-固体相互作用的有效方法，我们建立了一个完整的数值模型来模拟这一过程，并通过靶材在多次冲击下的表面变形进行了实验验证。根据模型详细分析了目标材料的动态响应，包括表面位移、应力和应变。研究发现，中心残余应力下降是由激光冲击的边界效应导致的反向塑性加载引起的。而采用方形激光光斑应能减弱释放波的同时聚焦，减少残余应力下降。

关键词：激光冲击强化残余应力数值模拟释放波

1.绪论

激光冲击强化（LSP）被视为一种具有竞争力的替代技术，能够取代传统处理方法，从而提升金属材料的抗疲劳、抗腐蚀和抗磨损性能。其对目标材料性能的改善，主要依靠冲击波所引发的机械效应实现，而非通过激光束对材料表面加热所产生的热效应。LSP尤其适用于对孔、缺口、圆角及焊缝等局部疲劳敏感区域进行精确处理。

针对铝合金、钢和钛合金等多种工业金属，已有大量实验致力于确定LSP处理后表面及内部的残余应力分布。研究表明，在典型的LSP处理中，处理区域内形成的压缩残余应力场呈现相对均匀的双轴分布特征。该残余应力通常在表面达到峰值，并随深度增加逐渐衰减。冲击压力越高，残余应力的幅值也随之增大，而冲击压力又与入射激光的强度密切相关。然而，即使激光强度超过一定阈值，冲击引起的残余应力场仍存在局部劣势，例如在激光作用区中心位置，残余应力反而偏低。这种残余应力分布的不均匀性尚未得到充分解释，但它有可能增强材料的抗疲劳能力，并更好地利用激光能量。这种现象与冲击波与固体材料之间的相互作用关系密切。由于材料对激光冲击的快速响应，实验上难以捕捉到瞬时的应力、应变以及表面位移等动态变化过程。因此，数值建模成为研究冲击—固体相互作用的有效工具。目前，已有诸多关于LSP的数值模拟研究，包括建模策略、双面冲击、多次冲击、微尺度LSP以及多次重叠冲击等。尽管这些研究主要关注如何准确预测残余应力场，但均证实数值模型能够有效捕捉激光产生的冲击波，并模拟其在各种金属材料中的传播行为。

在本研究中，开发了一个显式/隐式有限元模型，用于模拟激光冲击强化过程。为了探究激光冲击区中心残余应力偏低的成因，采用了显式动态模拟方法，并对表面位移、应力及应变等动态响应进行了深入分析。同时，通过模拟圆形与方形激光光斑的处理过程，系统研究了不同光斑形状所产生的边界效应。

2.LSP建模和验证2.1.数值建模

为了完整地对激光冲击强化（LSP）过程进行数值模拟，需要依次采用两个子模型。首先，使用约束等离子体发展模型预测激光条件下冲击压力的时间历程；随后，将该压力作为输入，通过有限元模型研究试样的机械响应。采用Fabbro提出的经典一维模型来预测冲击压力随时间的变化，同时考虑激光束的空间分布，假设冲击压力遵循高斯分布，其1/e²半径设为√2R，其中R为激光光斑半径。

有限元分析包括两个阶段：显式动态分析用于模拟冲击过程中的瞬态响应，隐式静态分析用于计算残余应力场。由于激光冲击载荷作用时间极短且压力极高，采用了简化的Johnson-Cook本构模型，以充分考虑高应变率对金属流动行为的影响。

其中，ε为无量纲应变率，A、B、C和n为材料常数。表1列出了有限元模拟所需的AISI 1045钢的材料属性。关于数值建模策略的详细描述，请参见之前发表的论文。

2.2.实验和验证

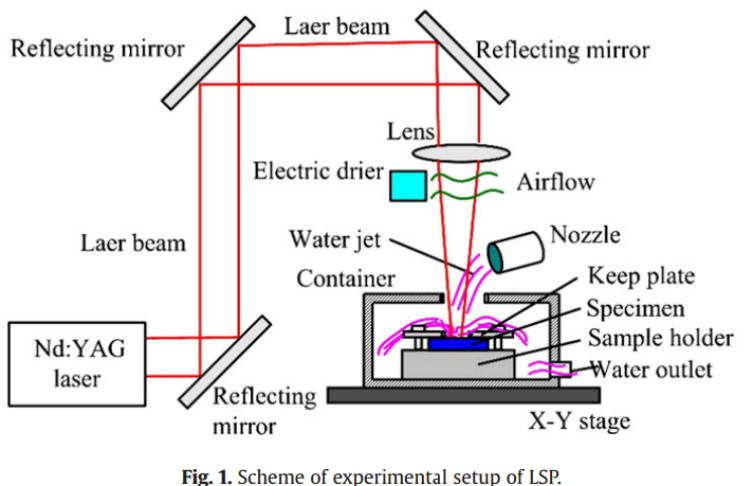
LSP实验使用Q开关Nd:YAG高功率脉冲激光器的二次谐波，波长为532nm，脉冲持续时间约10 ns，重复频率10 Hz。激光束空间分布为高斯型，黑色胶带（约109 μm厚）作为吸收层，水作为透明覆盖层以限制等离子体扩散。实验装置如图1所示，包括试样支架、位置控制平台、连续供水系统以及光学保护装置，详细参数可参考文献。通过会聚透镜聚焦激光束，得到光斑半径R=0.5 mm。实验选取两种输出脉冲能量：0.258 J和1.03 J，对应激光强度分别为约3.28 GW/cm²和13.12 GW/cm²。

由于激光冲击产生的残余应力测量存在一定的不确定性，特别是对于局部半径约0.5 mm的小区域而言，传统方法难以有效验证数值模型。然而，与残余应力密切相关的冲击区表面塑性变形测量具有更高的可靠性。图2展示了通过研磨和抛光预处理的1045钢试样表面，其变形通过Micro-XAM表面轮廓干涉仪进行测量。

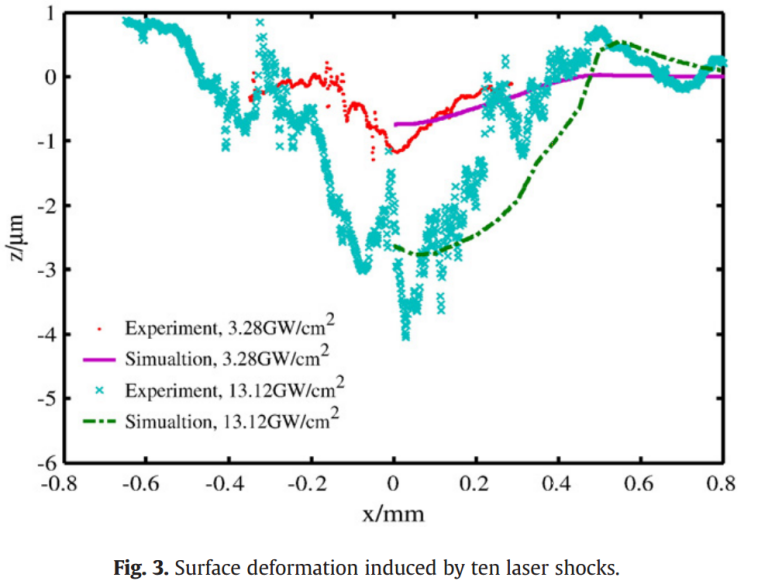
图3对比了模拟得到的塑性变形与不同激光强度下，经过10次冲击后的实验测量结果。尽管模拟与实验结果存在差异，但总体符合良好。实验中，冲击中心的变形略大于模拟值，主要原因在于激光中心热影响和烧蚀较轻，表面残留烧蚀物影响了测量，导致实验曲线不如模拟结果平滑。此外，实验与模拟中的变形梯度差异，可能源于实验中实际冲击压力沿径向的衰减速度比模型计算更快。

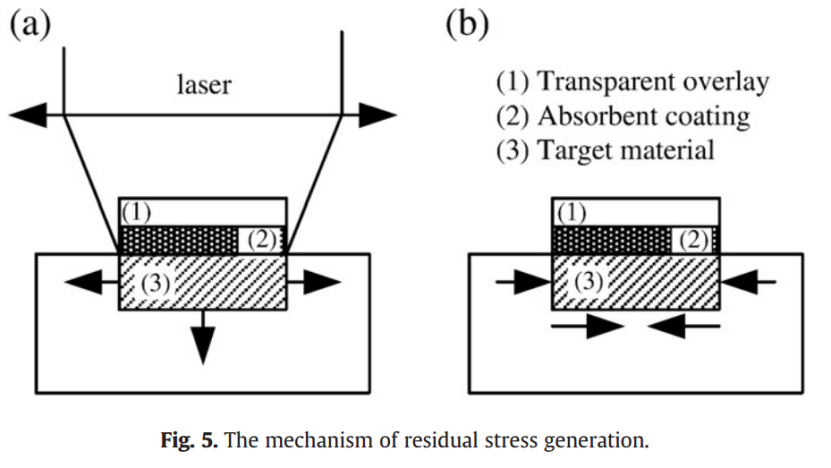
此外，研究计算了不同激光强度条件下，单次激光冲击产生的残余应力场。图4显示了顶面的模拟结果：3.28 GW/cm²激光强度下，压缩残余应力约为170 MPa；而13.12 GW/cm²激光强度下，则达到634 MPa。残余应力形成机制如图5所示。相互作用阶段（图5a），由于冲击波作用，撞击表面出现拉伸态。激光烧蚀结束后（图5b），周围材料响应体积变化，诱导形成双轴压应力场，从而恢复形状。因此，表面压缩残余应力的幅值随着激光诱导压力的升高而增加，而该压力又与入射激光强度直接相关。由于高斯型激光强度分布，冲击压力在光斑中心最大。在3.28 GW/cm²条件下，中心处残余压应力最高，向外径向逐渐降低。然而，在激光强度提升至13.12 GW/cm²时，中心残余应力反而低于周边区域。在更高的8 GPa冲击压力下，甚至出现拉伸残余应力，中心残余应力约为48 MPa拉伸态，这与A356-T6合金的实验结果一致，说明激光强度超过一定阈值后会引发此现象。实际上，残余应力场由激光诱导压力与材料相互作用直接决定。这一现象本质上源于靶材在高冲击压力作用下的动态响应，需借助显式动态模拟深入研究其机理。

3.动态响应分析3.1.位移和应力

事实上，由于各种应力波的反射与相互作用，靶材的响应变得非常复杂，需要更长时间才能达到稳定状态。这一现象主要表现为冲击中心的横向残余应力下降，因此，首先对顶面的动态横向位移（用ux表示）和横向应力（用sx表示）进行分析。模拟提取的结果如图6所示，其中坐标值x=0.05 mm代表最接近冲击中心的元素节点位置，而x=0.20 mm则对应图4所示在13.12 GW/cm²处理条件下顶面最大压缩残余应力的位置。

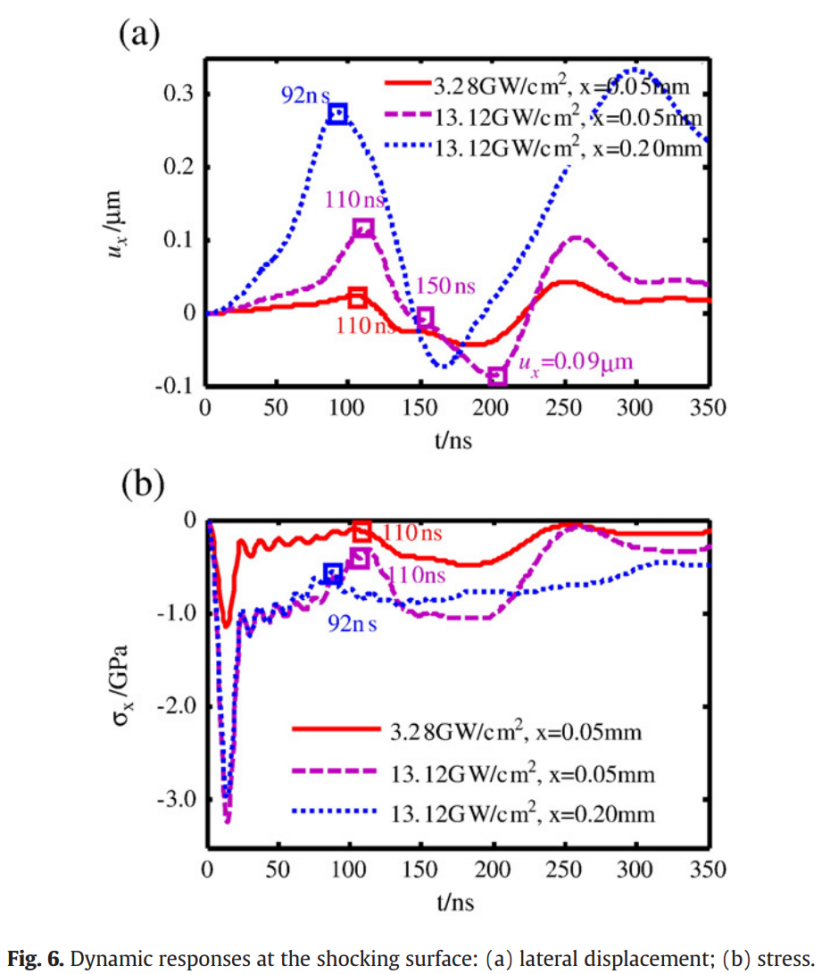
如图6a所示，材料颗粒的横向位移经历了动态变化。在冲击压力加载期间，随着材料表面沿纵向被压缩，横向位移随之增加。由于冲击压力的局部性，冲击区域外的颗粒对横向位移起到了限制作用。如图6b所示，冲击区内的应力呈压缩状态，并在加载过程中不断动态变化。在初始的松弛阶段，受运动惯性的影响，横向位移继续逐渐增加。在两种不同激光强度处理下，x=0.05 mm处的颗粒均在约110 ns时达到最大位移。随后，颗粒开始向光斑中心反向移动，导致位移逐渐减小，并引发横向的反向加载。当横向位移ux变为负值时，横向压应力随之减小，因为颗粒的反向运动削弱了对周围颗粒的约束作用。

通过对比图6a中反向加载阶段的动态横向位移，可以发现，在13.12 GW/cm²处理条件下，x=0.05 mm处的反向位移最大，约为-0.09 mm，对应的残余应力下降也最显著。这表明压应力的降低主要由反向加载引起。

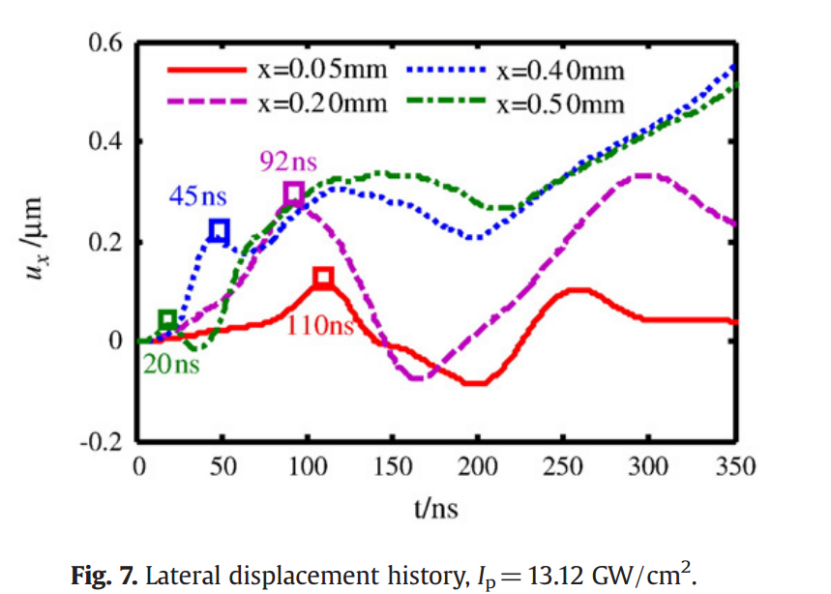
通过进一步分析冲击表面不同特征位置的动态位移，探讨反向加载产生的原因。如图7所示，位于x=0.05 mm、0.20 mm、0.40 mm和0.50 mm的位置，动态位移分别在110 ns、92 ns、45 ns和20 ns时达到峰值，然后开始减小，说明出现了反向位移。由于x=0.50 mm恰好位于光斑半径位置，因此反向加载引起的反向位移最先出现在激光冲击区边界，随后逐渐向冲击中心传递，诱发了Peyre等人提出的释放波。当释放波到达时，颗粒开始反向移动，横向位移减小。然而，当释放波到达激光冲击区中心后发生反射，颗粒再次远离中心移动，导致横向位移增加。这个过程会多次重复，并逐渐衰减。后续关于应变变化的讨论将进一步说明，在13.12 GW/cm²处理条件下，只有最初到达的释放波才会显著增加冲击中心的塑性应变。

3.2.应变

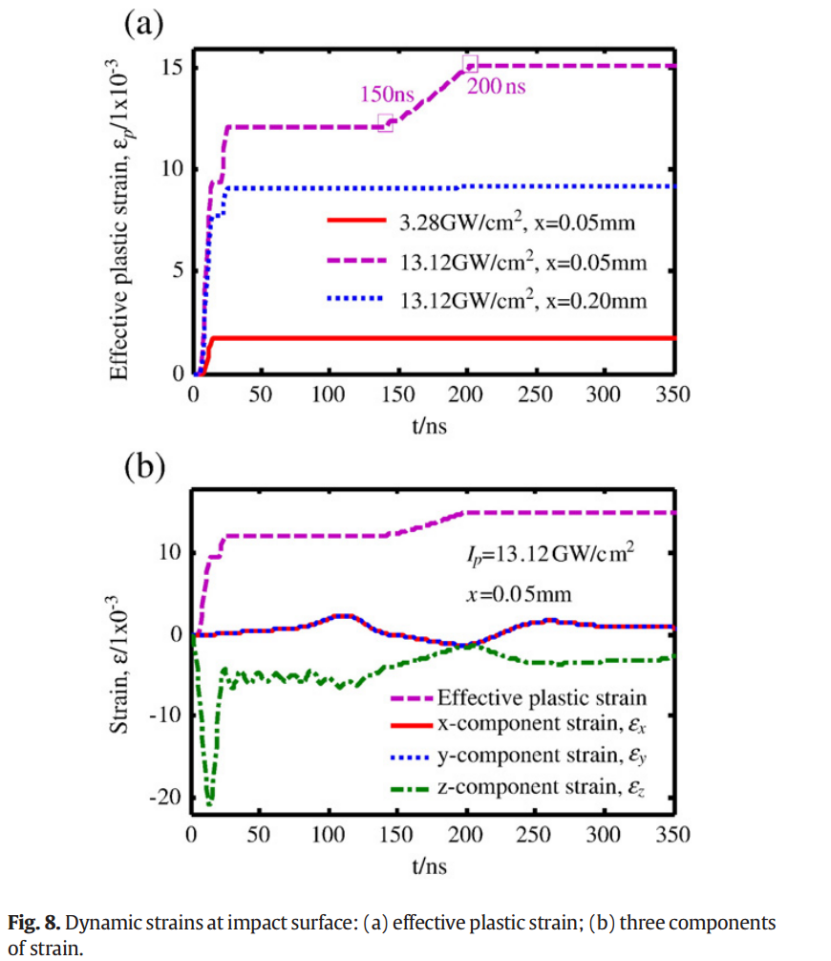
通过模拟获得动态应变分量的时间演化规律，以研究反向加载过程中弹塑性应变的转变行为。图8a展示了不同激光处理条件下的有效塑性应变变化情况。如图所示，在反向加载阶段，当反向位移呈负增长趋势（参见图6a）时，采用13.12 GW/cm²激光强度处理的试样在x=0.05 mm位置，于150 ns时出现了塑性应变的第二个增长台阶。相比之下，由于3.28 GW/cm²激光强度下的反向加载远弱于13.12 GW/cm²，相应的横向反向位移也显著较小，因此在该激光强度以及其他较低强度条件下，均未出现塑性应变的第二个增长台阶。

如图8b所示，在x=0.05 mm处进行13.12 GW/cm²处理时还形成了三轴主应变状态。反向加载后，横向应变（εx和εy）均为负值，而纵向应变（εz）则为正值，说明激光冲击区中心的颗粒在横向受到压缩。反向加载诱发的塑性变形发生在反方向，这种反向塑性变形减弱了周围颗粒对冲击中心颗粒的约束。如图4所示，在约8 GPa冲击压力作用下，如果这种变形达到一定程度，将会降低压应力，甚至可能导致拉应力的出现。因此，激光冲击区中心的残余应力下降，实际上是由冲击压力作用结束后发生的反向横向塑性变形所导致。

3.3.讨论

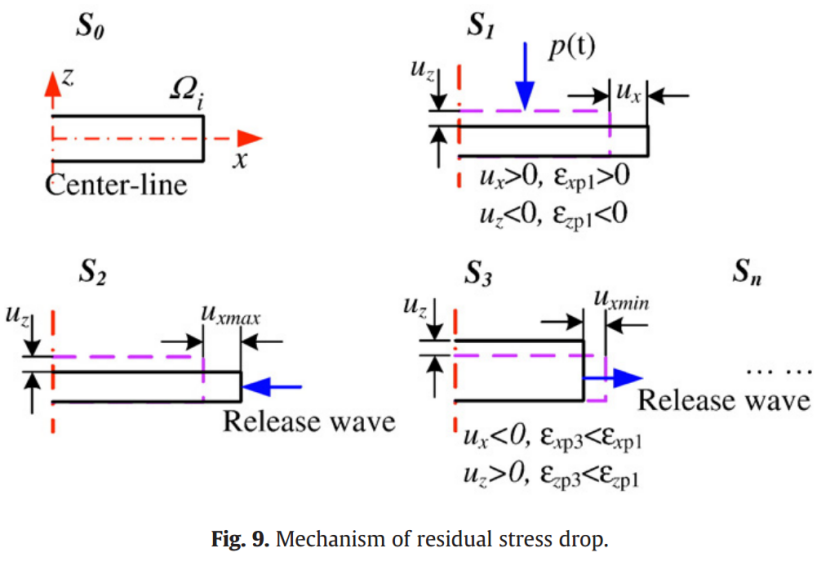
综上所述，激光冲击区中心低压缩残余应力的形成机制可以概括为图9所示：

(1)在初始状态S0的冲击压力加载下，冲击中心的粒子Ωi被压缩至状态S1，纵向（uz>0）呈现压缩状态，横向（ux> 0）则表现为膨胀，产生塑性应变εzp1>0。

(2)由于冲击压力的局部覆盖效应，粒子Ωi的横向膨胀受限于周围粒子的阻碍。来自激光冲击区边界的释放波开始向冲击中心传播。当冲击压力结束后，粒子Ωi继续膨胀，直到释放波到达其位置，达到最大横向位移uxmax，对应状态S2。

(3)在状态S2之后，表面释放波作用下，激光冲击区中心出现反向加载，使粒子Ωi进入状态S3。此时，横向表现为压缩（ux），纵向则呈现膨胀（uz>0）。如果冲击压力足够高，释放波将诱发粒子Ωi的强烈反向塑性变形，表现为εxp3> εxp1。

(4)随着粒子Ωi进入状态S3，其动态响应逐渐稳定，塑性变形不再增加。

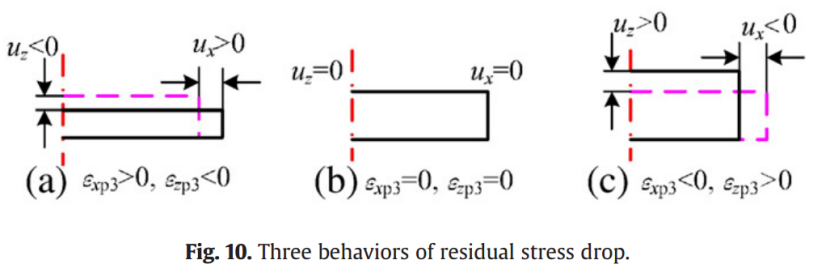
从状态S2向状态S3转变过程中发生的反向塑性变形，削弱了周围材料对粒子Ωi的横向约束，导致激光冲击区中心的压缩残余应力降低。正如参考文献所指出的，塑性应变与残余应力之间存在密切关系，且激光冲击区中心的压缩残余应力主导着这种关系。在文献中，塑性应变与应力关系表达式为：εp≈((σ-A)/B)1/2，其中εp是等效塑性应变。由于n>0，随着波压增大，释放波的强度增强，从而引发更大的塑性应变。因此，反向塑性变形与释放波强度紧密相关。如图10所示，残余应力下降在不同处理条件下表现为三种情形：

((1)如图10a，反向塑性变形较小。如果表面释放波较弱，稳定状态下的塑性应变εxp3> 0，εzp3> 0，残余应力依然为压应力，即激光冲击区中心的σx res> 0。

(2)如图10b，反向塑性变形较大。如果表面释放波相对较强，稳定状态下塑性应变趋近于零（εxp3 = 0，εzp3 = 0），残余应力也随之消失，即σx res= 0。

(3)如图10c，反向塑性变形极为显著。如果表面释放波非常强烈，稳定状态下的塑性应变表现为εxp3 < 0和εzp3 > 0，残余应力转为拉应力，即激光冲击区中心的σx res < 0，这对材料性能不利。

4.激光光斑形状的影响

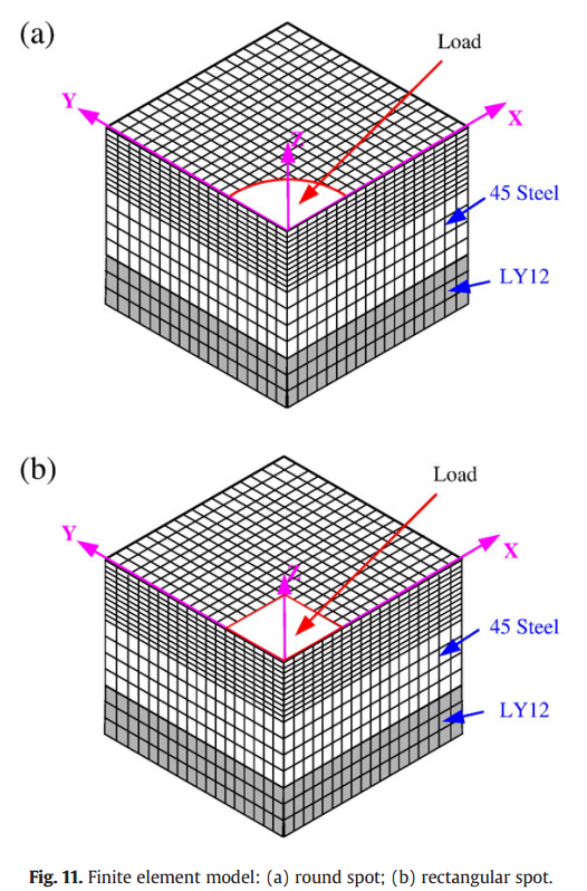
激光冲击区中心残余应力的降低，主要源于边界效应引发的反向塑性加载。因此，激光光斑的形状对残余应力场有着显著影响。为了研究圆形与方形激光光斑对残余应力分布的影响，采用了图11所示的数值模型进行分析。

如图12a所示，在约4 GPa均匀冲击压力作用下，圆形和方形激光光斑均在冲击区中心出现了残余应力降低的现象。然而，圆形光斑中心的残余应力约为-140 MPa，而方形光斑中心的残余应力则为-221 MPa，表明圆形激光光斑导致的残余应力下降程度更为严重。这一趋势与Peyre等人针对铸造铝合金的实验结果相一致。

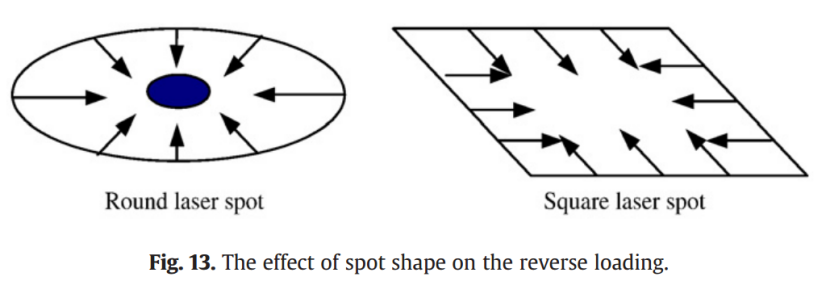
进一步分析如图12b所示，表面横向应变（εx）沿x轴的随时间变化规律可以看出，在反向加载阶段，圆形光斑产生的反向应变明显大于方形光斑。造成这一差异的原因在于，激光冲击边缘产生的径向释放波在相互作用后，会向中心聚焦，导致中心区域出现反向应变状态和残余应力的下降。如图13所示，采用圆形激光光斑时，来自圆周边缘的所有横向释放波均会汇聚至冲击中心，从而更容易引发残余应力的降低。而使用方形激光光斑时，释放波缺乏明显的聚焦效果，因此，中心区域的残余应力下降不如圆形光斑明显。

因此，采用方形激光光斑能够有效削弱释放波的聚焦效应，从而减缓激光冲击区中心的残余应力下降。结合不同激光强度下的动态响应分析可进一步确认，激光冲击中心区域的残余应力降低，正是由于边界效应引发的反向塑性加载所致。通过合理采用方形光斑，并进一步深入研究反向加载过程中的塑性变形控制策略，有望进一步减弱甚至消除中心残余应力的下降现象。

5.结论

冲击表面残余应力场的非均匀性，不利于试样获得均匀的疲劳性能，同时也不利于激光能量的充分利用。根据不同激光强度下动态响应的分析结果发现，激光冲击区中心残余应力的降低是由于激光冲击边界效应引发的反向塑性加载所致。采用方形激光光斑可以有效减弱释放波的同时聚焦效应。通过进一步研究反向加载过程中的塑性变形控制，并结合工艺参数优化、非圆形光斑设计以及激光冲击重叠策略，有望减弱甚至消除残余应力的降低现象。